CALCULO DE LA MEDIA, LA MEDIANA Y LA MODA (NO AGRUPADOS)
En una distribución de datos no agrupados, la media de obtiene mediante la formula:
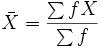 Donde X representa cada dato de la variable; F, la frecuencia que le corresponde y el total de datos (N). Para hallar la media se siguen dos pasos: se determina el número de orden que le corresponde sumando una unidad al total de los datos N y dividiéndolos entre dos:
Donde X representa cada dato de la variable; F, la frecuencia que le corresponde y el total de datos (N). Para hallar la media se siguen dos pasos: se determina el número de orden que le corresponde sumando una unidad al total de los datos N y dividiéndolos entre dos:Y se construye una distribución de frecuencias acumuladas, ascendente o descendente. La mediana es el dato de la variable cuya frecuencia acumulada contiene o señala su número ordinal.
Y es la moda el dato de mayor frecuencia.
Resulta ventajoso llenar primero una estructura donde todos ellos aparezcan claramente y hacer posteriormente las sustituciones y lecturas que se necesiten. La estructura es la siguiente:
Datos F D.F.A FX
CALCULO DE LA MEDIA, LA MEDIANA Y LA MODA
Una distribución de datos en clase se convierte en una distribución simple de frecuencias y por ende, la formula para calcular la media en esta ultima distribución es valida para calcular en aquella.
Donde x es la marca de clase o punto medio de cada intervalo; f, su frecuencia. Es natural, entonces que el primer paso para calcular la media sea hallar los puntos medios de cada intervalo.
La media estará en el intervalo cuya frecuencia acumulada sea inmediatamente mayor a la mitad de los datos de la distribución. Pero es necesario seguir un procedimiento de interpolación que parte del supuesto de que todos los valores dentro del intervalo están distribuidos de manera uniforme. Tal procedimiento conduce a la formula:
Donde N es el total de datos de la distribución; Y, referidos exclusivamente al intervalo donde cae la mediana, L es el limite real inferíos; Σ fd, la frecuencia acumulada inmediatamente menor a la del intervalo; fj, la frecuencia y J, la anchura real.
Respecto a la moda, identificaremos su valor con el punto medio del intervalo de mayor frecuencia.
Para calcular la media y la mediana se llevara primero un cuadro donde aquellos aparezcan claramente y se harán luego las sustituciones de rigor para cada caso.
L A MEDIA, LA MEDIANA Y LA MODA EN VARIABLE NOMINAL Y ORDINAL.
Surge ahora la pregunta de si la media, la mediana y la moda son calculables en los otros dos tipos de variable. Para responder con fundamentos basta con conocer las características de las nominales y las ordinales y las propiedades de los símbolos asignados a sus categorías, asi como lo inherente a las operaciones que conducen a los valores de la media, la mediana y la moda. Las variables nominales son simplemente clasificadores por que, al medirlas es una escala adecuada, resulta una clasificación de las observaciones en un conjunto de categorías mutuamente excluyentes, que no requieren de orden alguno para conseguir claridad y coherencia. Una variable es ordinal por que sus categorías guardan relaciones de “mayor que “, lo cual exige que se les de el orden apropiado. La moda: como ella depende de las frecuencias de las clases o categorías de la variable, y no de los valores absolutos de estas, es claro que puede ser determinada en variable nominal y ordinal.





No hay comentarios:
Publicar un comentario