domingo, 2 de diciembre de 2007
PROPORCIONE LA DESVIACIONY MTC ASI COMO UNA FUNCION ESTADISTICA EN EL ESTUDIO DE LA SIGUIENTE VARIABLE: NUMERO DE HERMANOS DE ALUMNOS DEL 5º"A"
DETERMINE LA MTC Y MD ASI COMO SU ANALISIS ESTADISTICO DE: PROPORCION DE AZUCAR EB TODOS LOS INGENIEROS DEL PAIS , MEXICO ZAFRA 89/90



sábado, 1 de diciembre de 2007
RESUMEN
CALCULO DE LA MEDIA, LA MEDIANA Y LA MODA (NO AGRUPADOS)
En una distribución de datos no agrupados, la media de obtiene mediante la formula:
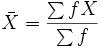 Donde X representa cada dato de la variable; F, la frecuencia que le corresponde y el total de datos (N). Para hallar la media se siguen dos pasos: se determina el número de orden que le corresponde sumando una unidad al total de los datos N y dividiéndolos entre dos:
Donde X representa cada dato de la variable; F, la frecuencia que le corresponde y el total de datos (N). Para hallar la media se siguen dos pasos: se determina el número de orden que le corresponde sumando una unidad al total de los datos N y dividiéndolos entre dos:Y se construye una distribución de frecuencias acumuladas, ascendente o descendente. La mediana es el dato de la variable cuya frecuencia acumulada contiene o señala su número ordinal.
Y es la moda el dato de mayor frecuencia.
Resulta ventajoso llenar primero una estructura donde todos ellos aparezcan claramente y hacer posteriormente las sustituciones y lecturas que se necesiten. La estructura es la siguiente:
Datos F D.F.A FX
CALCULO DE LA MEDIA, LA MEDIANA Y LA MODA
Una distribución de datos en clase se convierte en una distribución simple de frecuencias y por ende, la formula para calcular la media en esta ultima distribución es valida para calcular en aquella.
Donde x es la marca de clase o punto medio de cada intervalo; f, su frecuencia. Es natural, entonces que el primer paso para calcular la media sea hallar los puntos medios de cada intervalo.
La media estará en el intervalo cuya frecuencia acumulada sea inmediatamente mayor a la mitad de los datos de la distribución. Pero es necesario seguir un procedimiento de interpolación que parte del supuesto de que todos los valores dentro del intervalo están distribuidos de manera uniforme. Tal procedimiento conduce a la formula:
Donde N es el total de datos de la distribución; Y, referidos exclusivamente al intervalo donde cae la mediana, L es el limite real inferíos; Σ fd, la frecuencia acumulada inmediatamente menor a la del intervalo; fj, la frecuencia y J, la anchura real.
Respecto a la moda, identificaremos su valor con el punto medio del intervalo de mayor frecuencia.
Para calcular la media y la mediana se llevara primero un cuadro donde aquellos aparezcan claramente y se harán luego las sustituciones de rigor para cada caso.
L A MEDIA, LA MEDIANA Y LA MODA EN VARIABLE NOMINAL Y ORDINAL.
Surge ahora la pregunta de si la media, la mediana y la moda son calculables en los otros dos tipos de variable. Para responder con fundamentos basta con conocer las características de las nominales y las ordinales y las propiedades de los símbolos asignados a sus categorías, asi como lo inherente a las operaciones que conducen a los valores de la media, la mediana y la moda. Las variables nominales son simplemente clasificadores por que, al medirlas es una escala adecuada, resulta una clasificación de las observaciones en un conjunto de categorías mutuamente excluyentes, que no requieren de orden alguno para conseguir claridad y coherencia. Una variable es ordinal por que sus categorías guardan relaciones de “mayor que “, lo cual exige que se les de el orden apropiado. La moda: como ella depende de las frecuencias de las clases o categorías de la variable, y no de los valores absolutos de estas, es claro que puede ser determinada en variable nominal y ordinal.
domingo, 23 de septiembre de 2007
sábado, 1 de septiembre de 2007
ACTIVIDAD 1
L a población de San Mateo Atenco consta de 1, 486,000 habitantes de los cuales el
52% son hombres y el resto son mujeres.
El presidente municipal de la comunidad desea saber como y cuando construirá una escuela secundaria, un bachillerato y una facultad.
PROPORCIONE LO SIGUIENTE:
a) Universo del estudio: San Mateo Atenco.
b) Población: Habitantes.
c) Muestra: 1 Habitante.
d) Qué se desea investigar: Edad de los habitantes.
e) Que información le será útil: Saber el número de habitantes que hay en un cierto intervalo de edad.
f) Diga como obtendría usted estos datos: Con una encuesta.
L a población de San Mateo Atenco consta de 1, 486,000 habitantes de los cuales el
52% son hombres y el resto son mujeres.
El presidente municipal de la comunidad desea saber como y cuando construirá una escuela secundaria, un bachillerato y una facultad.
PROPORCIONE LO SIGUIENTE:
a) Universo del estudio: San Mateo Atenco.
b) Población: Habitantes.
c) Muestra: 1 Habitante.
d) Qué se desea investigar: Edad de los habitantes.
e) Que información le será útil: Saber el número de habitantes que hay en un cierto intervalo de edad.
f) Diga como obtendría usted estos datos: Con una encuesta.
viernes, 31 de agosto de 2007
Conceptos Básicos
Estadística
La estadística es comúnmente considerada como una colección de hechos numéricos expresados en términos de una relación sumisa, y que han sido recopilado a partir de otros datos numéricos.
Kendall y Buckland (citados por Gini V. Glas / Julian C. Stanley, 1980) definen la estadística como un valor resumido, calculado, como base en una muestra de observaciones que generalmente, aunque no por necesidad, se considera como una estimación de parámetro de determinada población; es decir, una función de valores de muestra.
"La estadística es una técnica especial apta para el estudio cuantitativo de los fenómenos de masa o colectivo, cuya mediación requiere una masa de observaciones de otros fenómenos más simples llamados individuales o particulares". (Gini, 1953.
Murria R. Spiegel, (1991) dice: "La estadística estudia los métodos científicos para recoger, organizar, resumir y analizar datos, así como para sacar conclusiones válidas y tomar decisiones razonables basadas en tal análisis.
"La estadística es la ciencia que trata de la recolección, clasificación y presentación de los hechos sujetos a una apreciación numérica como base a la explicación, descripción y comparación de los fenómenos". (Yale y Kendal, 1954).
Cualquiera sea el punto de vista, lo fundamental es la importancia científica que tiene la estadística, debido al gran campo de aplicación que posee.
Población
El concepto de población en estadística va más allá de lo que comúnmente se conoce como tal. Una población se precisa como un conjunto finito o infinito de personas u objetos que presentan características comunes.
"Una población es un conjunto de todos los elementos que estamos estudiando, acerca de los cuales intentamos sacar conclusiones". Levin & Rubin (1996).
"Una población es un conjunto de elementos que presentan una característica común". Cadenas (1974).
Ejemplo:
Los miembros del Colegio de Ingenieros del Estado Cojedes.
El tamaño que tiene una población es un factor de suma importancia en el proceso de investigación estadística, y este tamaño vienen dado por el número de elementos que constituyen la población, según el número de elementos la población puede ser finita o infinita. Cuando el número de elementos que integra la población es muy grande, se puede considerar a esta como una población infinita, por ejemplo; el conjunto de todos los números positivos. Una población finita es aquella que está formada por un limitado número de elementos, por ejemplo; el número de estudiante del Núcleo San Carlos de la Universidad Nacional Experimental Simón Rodríguez.
Cuando la población es muy grande, es obvio que la observación de todos los elementos se dificulte en cuanto al trabajo, tiempo y costos necesario para hacerlo. Para solucionar este inconveniente se utiliza una muestra estadística.
Es a menudo imposible o poco práctico observar la totalidad de los individuos, sobre todos si estos son muchos. En lugar de examinar el grupo entero llamado población o universo, se examina una pequeña parte del grupo llamada muestra.
Muestra
"Se llama muestra a una parte de la población a estudiar que sirve para representarla". Murria R. Spiegel (1991).
"Una muestra es una colección de algunos elementos de la población, pero no de todos". Levin & Rubin (1996).
"Una muestra debe ser definida en base de la población determinada, y las conclusiones que se obtengan de dicha muestra solo podrán referirse a la población en referencia", Cadenas (1974).
Ejemplo;
El estudio realizado a 50 miembros del Colegio de Ingenieros del Estado Cojedes.
El estudio de muestras es más sencillo que el estudio de la población completa; cuesta menos y lleva menos tiempo. Por último se aprobado que el examen de una población entera todavía permite la aceptación de elementos defectuosos, por tanto, en algunos casos, el muestreo puede elevar el nivel de calidad.
Una muestra representativa contiene las características relevantes de la población en las mismas proporciones que están incluidas en tal población.
Los expertos en estadística recogen datos de una muestra. Utilizan esta información para hacer referencias sobre la población que está representada por la muestra. En consecuencia muestra y población son conceptos relativos. Una población es un todo y una muestra es una fracción o segmento de ese todo.
Muestreo
Esto no es más que el procedimiento empleado para obtener una o más muestras de una población; el muestreo es una técnica que sirve para obtener una o más muestras de población.
Este se realiza una vez que se ha establecido un marco muestral representativo de la población, se procede a la selección de los elementos de la muestra aunque hay muchos diseños de la muestra.
Al tomar varias muestras de una población, las estadísticas que calculamos para cada muestra no necesariamente serían iguales, y lo más probable es que variaran de una muestra a otra.
Ejemplo
Consideremos como una población a los estudiantes de educación del Núcleo San Carlos de la UNESR, determinando por lo menos dos caracteres ser estudiados en dicha población;
• Religión de los estudiantes
• Sexo.
Tipos de muestreo
Existen dos métodos para seleccionar muestras de poblaciones; el muestreo no aleatorio o de juicio y el muestreo aleatorio o de probabilidad. En este último todos los elementos de la población tienen la oportunidad de ser escogidos en la muestra. Una muestra seleccionada por muestreo de juicio se basa en la experiencia de alguien con la población. Algunas veces una muestra de juicio se usa como guía o muestra tentativa para decidir como tomar una muestra aleatoria más adelante. Las muestras de juicio evitan el análisis estadístico necesarios para hacer muestras de probabilidad.
Variables y Atributos
Las variables, también suelen ser llamados caracteres cuantitativos, son aquellos que pueden ser expresados mediante números. Son caracteres susceptibles de medición. Como por ejemplo, la estatura, el peso, el salario, la edad, etc.
Según, Murray R. Spiegel, (1992) "una variable es un símbolo, tal como X, Y, Hx, que puede tomar un valor cualquiera de un conjunto determinado de ellos, llamado dominio de la variable. Si la variable puede tomar solamente un valor, se llama constante."
Todos los elementos de la población poseen los mismos tipos de caracteres, pero como estos en general no suelen representarse con la misma intensidad, es obvio que las variables toman distintos valores. Por lo tanto estos distintos números o medidas que toman los caracteres son los "valores de la variable". Todos ellos juntos constituyen una variable.
Los atributos también llamados caracteres cualitativos, son aquellos que no son susceptibles de medición, es decir que no se pueden expresar mediante un número.
IUTIN (1997). "Reciben el nombre de variables cualitativas o atributos, aquellas características que pueden presentarse en individuos que constituyen un conjunto.
La forma de expresar los atributos es mediante palabras, por ejemplo; profesión, estado civil, sexo, nacionalidad, etc. Puede notar que los atributos no se presentan en la misma forma en todos los elementos. Estas distintas formas en que se presentan los atributos reciben el nombre de "modalidades".
Estadística
La estadística es comúnmente considerada como una colección de hechos numéricos expresados en términos de una relación sumisa, y que han sido recopilado a partir de otros datos numéricos.
Kendall y Buckland (citados por Gini V. Glas / Julian C. Stanley, 1980) definen la estadística como un valor resumido, calculado, como base en una muestra de observaciones que generalmente, aunque no por necesidad, se considera como una estimación de parámetro de determinada población; es decir, una función de valores de muestra.
"La estadística es una técnica especial apta para el estudio cuantitativo de los fenómenos de masa o colectivo, cuya mediación requiere una masa de observaciones de otros fenómenos más simples llamados individuales o particulares". (Gini, 1953.
Murria R. Spiegel, (1991) dice: "La estadística estudia los métodos científicos para recoger, organizar, resumir y analizar datos, así como para sacar conclusiones válidas y tomar decisiones razonables basadas en tal análisis.
"La estadística es la ciencia que trata de la recolección, clasificación y presentación de los hechos sujetos a una apreciación numérica como base a la explicación, descripción y comparación de los fenómenos". (Yale y Kendal, 1954).
Cualquiera sea el punto de vista, lo fundamental es la importancia científica que tiene la estadística, debido al gran campo de aplicación que posee.
Población
El concepto de población en estadística va más allá de lo que comúnmente se conoce como tal. Una población se precisa como un conjunto finito o infinito de personas u objetos que presentan características comunes.
"Una población es un conjunto de todos los elementos que estamos estudiando, acerca de los cuales intentamos sacar conclusiones". Levin & Rubin (1996).
"Una población es un conjunto de elementos que presentan una característica común". Cadenas (1974).
Ejemplo:
Los miembros del Colegio de Ingenieros del Estado Cojedes.
El tamaño que tiene una población es un factor de suma importancia en el proceso de investigación estadística, y este tamaño vienen dado por el número de elementos que constituyen la población, según el número de elementos la población puede ser finita o infinita. Cuando el número de elementos que integra la población es muy grande, se puede considerar a esta como una población infinita, por ejemplo; el conjunto de todos los números positivos. Una población finita es aquella que está formada por un limitado número de elementos, por ejemplo; el número de estudiante del Núcleo San Carlos de la Universidad Nacional Experimental Simón Rodríguez.
Cuando la población es muy grande, es obvio que la observación de todos los elementos se dificulte en cuanto al trabajo, tiempo y costos necesario para hacerlo. Para solucionar este inconveniente se utiliza una muestra estadística.
Es a menudo imposible o poco práctico observar la totalidad de los individuos, sobre todos si estos son muchos. En lugar de examinar el grupo entero llamado población o universo, se examina una pequeña parte del grupo llamada muestra.
Muestra
"Se llama muestra a una parte de la población a estudiar que sirve para representarla". Murria R. Spiegel (1991).
"Una muestra es una colección de algunos elementos de la población, pero no de todos". Levin & Rubin (1996).
"Una muestra debe ser definida en base de la población determinada, y las conclusiones que se obtengan de dicha muestra solo podrán referirse a la población en referencia", Cadenas (1974).
Ejemplo;
El estudio realizado a 50 miembros del Colegio de Ingenieros del Estado Cojedes.
El estudio de muestras es más sencillo que el estudio de la población completa; cuesta menos y lleva menos tiempo. Por último se aprobado que el examen de una población entera todavía permite la aceptación de elementos defectuosos, por tanto, en algunos casos, el muestreo puede elevar el nivel de calidad.
Una muestra representativa contiene las características relevantes de la población en las mismas proporciones que están incluidas en tal población.
Los expertos en estadística recogen datos de una muestra. Utilizan esta información para hacer referencias sobre la población que está representada por la muestra. En consecuencia muestra y población son conceptos relativos. Una población es un todo y una muestra es una fracción o segmento de ese todo.
Muestreo
Esto no es más que el procedimiento empleado para obtener una o más muestras de una población; el muestreo es una técnica que sirve para obtener una o más muestras de población.
Este se realiza una vez que se ha establecido un marco muestral representativo de la población, se procede a la selección de los elementos de la muestra aunque hay muchos diseños de la muestra.
Al tomar varias muestras de una población, las estadísticas que calculamos para cada muestra no necesariamente serían iguales, y lo más probable es que variaran de una muestra a otra.
Ejemplo
Consideremos como una población a los estudiantes de educación del Núcleo San Carlos de la UNESR, determinando por lo menos dos caracteres ser estudiados en dicha población;
• Religión de los estudiantes
• Sexo.
Tipos de muestreo
Existen dos métodos para seleccionar muestras de poblaciones; el muestreo no aleatorio o de juicio y el muestreo aleatorio o de probabilidad. En este último todos los elementos de la población tienen la oportunidad de ser escogidos en la muestra. Una muestra seleccionada por muestreo de juicio se basa en la experiencia de alguien con la población. Algunas veces una muestra de juicio se usa como guía o muestra tentativa para decidir como tomar una muestra aleatoria más adelante. Las muestras de juicio evitan el análisis estadístico necesarios para hacer muestras de probabilidad.
Variables y Atributos
Las variables, también suelen ser llamados caracteres cuantitativos, son aquellos que pueden ser expresados mediante números. Son caracteres susceptibles de medición. Como por ejemplo, la estatura, el peso, el salario, la edad, etc.
Según, Murray R. Spiegel, (1992) "una variable es un símbolo, tal como X, Y, Hx, que puede tomar un valor cualquiera de un conjunto determinado de ellos, llamado dominio de la variable. Si la variable puede tomar solamente un valor, se llama constante."
Todos los elementos de la población poseen los mismos tipos de caracteres, pero como estos en general no suelen representarse con la misma intensidad, es obvio que las variables toman distintos valores. Por lo tanto estos distintos números o medidas que toman los caracteres son los "valores de la variable". Todos ellos juntos constituyen una variable.
Los atributos también llamados caracteres cualitativos, son aquellos que no son susceptibles de medición, es decir que no se pueden expresar mediante un número.
IUTIN (1997). "Reciben el nombre de variables cualitativas o atributos, aquellas características que pueden presentarse en individuos que constituyen un conjunto.
La forma de expresar los atributos es mediante palabras, por ejemplo; profesión, estado civil, sexo, nacionalidad, etc. Puede notar que los atributos no se presentan en la misma forma en todos los elementos. Estas distintas formas en que se presentan los atributos reciben el nombre de "modalidades".
jueves, 30 de agosto de 2007
Suscribirse a:
Comentarios (Atom)